[Java/자료구조] 우선순위 큐(PriorityQueue)와 힙(Heap)

서론

지난 Stack vs Queue 포스팅에 이어서 java.util.* 패키지에 구현된 PriorityQueue와 내부 구현 자료구조인 Heap에 대해서 알아보고자 한다.

정의

PriorityQueue

우선순위 큐는 큐에 원소 별로 ‘우선순위’라는 개념을 도입한 자료구조를 의미한다.

구현 방식에 따른 시간 복잡도

구현 방법	enqueue() 삽입	dequeue() 삭제
배열 (unsorted array)	O(1)	O(N)
연결 리스트(unsorted linked list)	O(1)	O(N)
정렬된 배열(sorted array)	O(N)	O(1)
정렬된 연결 리스트 (sorted linked list)	O(N)	O(1)
힙 (heap)	O(logN)	O(logN)

다양한 방식으로 우선순위 큐를 구현할 수 있지만 그 중에 힙으로 구현한 우선순위 큐가 삽입, 삭제에 대해서 O(logN)으로 가장 효율적이다. 바로 힙이 어떤 자료구조인지 알아보자.

힙과 트리

힙은 완전 이진 트리로 이루어져있고, 부모 노드가 자식 노드보다 커야하는 최대 힙과, 반대로 부모 노드가 자식 노드보다 작아야하는 최소 힙과 같이 특수한 조건의 트리이다.
완전 이진 트리란, 마지막 레벨의 노드를 제외하고 그 윗 레벨의 노드들은 모두 자식 노드가 2개씩 꽉 차있어야하는 조건의 이진 트리다.

힙에서 데이터의 삽입과 삭제

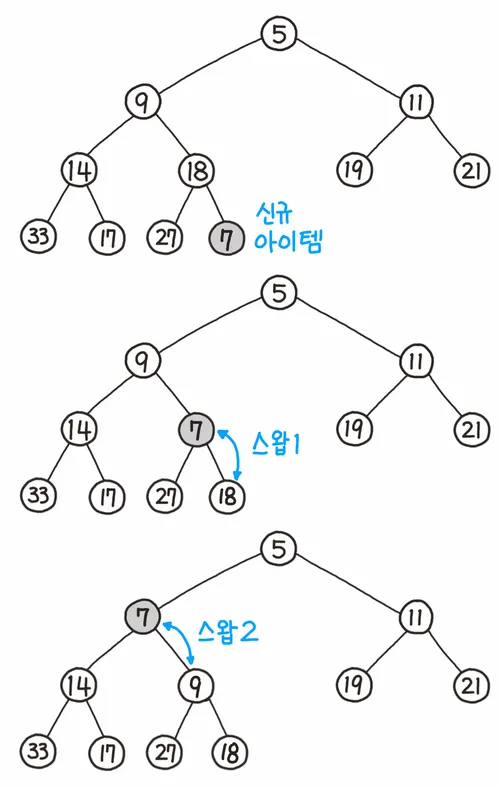
💡 특수한 트리 형태의 힙 자료구조에서 데이터가 삽입, 삭제될 때 내부적으로 어떤 로직이 동작하는 지 보자.

데이터의 삽입

1. 가장 끝의 자리에 노드를 삽입한다.
2. 그 노드와 부모 노드를 서로 비교한다.
3. 규칙에 맞으면 그대로 두고, 그렇지 않으면 부모와 교환한다. (부모 노드는 삽입된 위치의 인덱스 번호에서 /2를 하면 쉽게 구할 수 있다.)
4. 규칙에 맞을 때까지 3번 과정을 반복한다.

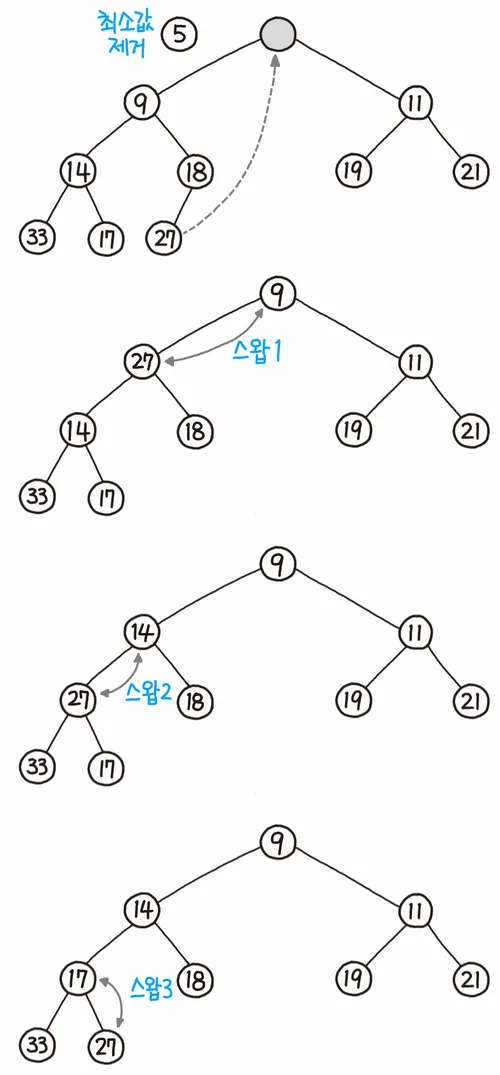
데이터의 삭제

1. 루트 노드를 제거한다.
2. 루트 자리에 가장 마지막 노드를 삽입한다.
3. 올라간 노드와 그의 자식 노드(들)와 비교한다.
4. 조건에 만족하면 그대로 두고, 그렇지 않으면 자식과 교환한다.
   • 최대 힙
     1. 부모보다 더 큰 자식이 없으면 교환하지 않고 끝낸다.
     2. 부모보다 더 큰 자식이 하나만 있으면 그 자식하고 교환하면 된다.
     3. 부모보다 더 큰 자식이 둘 있으면 자식들 중 큰 값과 교환한다.
   • 최소 힙
     1. 부모보다 더 작은 자식이 없으면 교환하지 않고 끝낸다.
     2. 부모보다 더 작은 자식이 하나만 있으면 그 자식하고 교환하면 된다.
     3. 부모보다 더 작은 자식이 둘 있으면 자식들 중 작은 값과 교환한다.
5. 조건을 만족할 때까지 4의 과정을 반복한다.

배열로 이루어진 Heap

⚠️ 힙은 보통 배열로 구현되어져 있는데 트리 형태의 힙을 배열로 관리하려면 인덱스를 아래의 기준으로 부모와 자식 노드의 위치를 찾을 수 있다.
루트 노드는 편의 상 인덱스 1로 설정하고,
왼쪽 자식 노드는 (parent * 2) 인덱스로 나타내고,
오른쪽 자식 노드는 (parent * 2) + 1로 나타낸다.
현재 노드의 부모 노드는 (child - 1) / 2로 찾을 수 있다.
⚠️ 실제 Java의 PriorityQueue는 배열의 0번 인덱스부터 데이터를 저장한다.

힙의 활용 사례

• 우선순위 큐
• 다익스트라 알고리즘(최단 경로 찾을 때)
• 힙 정렬 (heap sort)
• 허프만 코드
• CPU 스케줄링 (예상 소요 시간, 중요도 우선순위 기반 정렬)

⚠️ Java의 메모리 구조 중 객체를 관리할 때 사용되는 힙 영역은 힙 자료구조와는 관련이 없다.

Java의 PriorityQueue

PriorityQueue.java에서 데이터는 어떤 타입, 클래스로 관리되어질까?

java.util.PriorityQueue 클래스를 통해 Java util 패키지에서 우선순위 큐가 어떻게 구현되어있는지 보려고 한다.

public class PriorityQueue<E> extends AbstractQueue<E> implements java.io.Serializable {
    transient Object[] queue; // non-private to simplify nested class access
    //...
}

위 코드에서 우선순위 큐 내에서 사용되는 힙은 배열로 관리되어있다는 점을 알 수 있다.

PriorityQueue.java에서 데이터의 삽입과 삭제는 어떻게 구현되어 있을까?

먼저 데이터의 삽입 부터 살펴보면, PriorityQueue.java에서 삽입에 대한 메소드는 offer()와 add()로 구성되어있다.

public class PriorityQueue<E> extends AbstractQueue<E>
    implements java.io.Serializable {
    //...
    public boolean add(E e) {
        return offer(e);
    }

    public boolean offer(E e) {
        if (e == null)
            throw new NullPointerException();
        modCount++;
        int i = size;
        if (i >= queue.length)
            grow(i + 1);
        siftUp(i, e);
        size = i + 1;
        return true;
    }
    //...
}

내부의 grow() 메소드는 내부적으로 PriorityQueue에서 관리되어지는 배열의 크기가 꽉 찼을 때 공간을 늘려주는 부분의 메소드이다.
siftUp() 메소드에서 위의 힙 내에서 삽입 로직(heapify)이 일어나게 되며 아래와 같이 Comparator가 구현된 객체와 아닌 제네릭(T)에 따라 다른 메소드가 실행된다.

public class PriorityQueue<E> extends AbstractQueue<E> implements java.io.Serializable {
    //...
    private static <T> void siftUpComparable(int k, T x, Object[] es) {
        Comparable<? super T> key = (Comparable<? super T>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = es[parent];
            if (key.compareTo((T) e) >= 0)
                break;
            es[k] = e;
            k = parent;
        }
        es[k] = key;
    }

    private static <T> void siftUpUsingComparator(
        int k, T x, Object[] es, Comparator<? super T> cmp) {
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = es[parent];
            if (cmp.compare(x, (T) e) >= 0)
                break;
            es[k] = e;
            k = parent;
        }
        es[k] = x;
    }
    //...
}

인덱스 기반 (x »> 1 == x / 2) 계산으로 부모 노드의 값과 현재(자식) 노드의 값을 비교하며 swap이 필요하다면 swap을 하는 로직을 볼 수 있다.

그리고 다음으로 힙에서 데이터가 삭제되는(root 노드의 값이 꺼내지는) 부분에 대해서 보면, PriorityQueue.java에서 삭제에 대한 메소드는 poll()로 이루어져있다.

public class PriorityQueue<E> extends AbstractQueue<E> implements java.io.Serializable {
    //...
    public E poll() {
        final Object[] es;
        final E result;

        if ((result = (E) ((es = queue)[0])) != null) {
            modCount++;
            final int n;
            final E x = (E) es[(n = --size)];
            es[n] = null;
            if (n > 0) {
                final Comparator<? super E> cmp;
                if ((cmp = comparator) == null)
                    siftDownComparable(0, x, es, n);
                else
                    siftDownUsingComparator(0, x, es, n, cmp);
            }
        }
        return result;
    }
    //...
    private static <T> void siftDownComparable(int k, T x, Object[] es, int n) {
        // assert n > 0;
        Comparable<? super T> key = (Comparable<? super T>)x;
        int half = n >>> 1;           // loop while a non-leaf
        while (k < half) {
            int child = (k << 1) + 1; // assume left child is least
            Object c = es[child];
            int right = child + 1;
            if (right < n &&
                ((Comparable<? super T>) c).compareTo((T) es[right]) > 0)
                c = es[child = right];
            if (key.compareTo((T) c) <= 0)
                break;
            es[k] = c;
            k = child;
        }
        es[k] = key;
    }

    private static <T> void siftDownUsingComparator(
        int k, T x, Object[] es, int n, Comparator<? super T> cmp) {
        // assert n > 0;
        int half = n >>> 1;
        while (k < half) {
            int child = (k << 1) + 1;
            Object c = es[child];
            int right = child + 1;
            if (right < n && cmp.compare((T) c, (T) es[right]) > 0)
                c = es[child = right];
            if (cmp.compare(x, (T) c) <= 0)
                break;
            es[k] = c;
            k = child;
        }
        es[k] = x;
    }
    //...
}

queue[0]의 값을 먼저 result 변수에 저장한 뒤, 위에서 본 힙의 삭제 로직(heapify)처럼 배열의 마지막 인덱스 값을 루트로 올린다.
그 후, 자식 노드들과 값을 비교하면서 왼쪽 자식 노드와 오른쪽 자식 노드들 중 정렬의 우선순위가 높은 값의 자식 노드와 swap하면서 적당한 위치를 찾아간다.

힙 정렬

1. 원소들을 전부 힙에 삽입한다.
2. 힙의 루트에 있는 값은 남은 수들 중에서 최솟값(혹은 최댓값)을 가지므로 루트를 출력하고 힙에서 제거한다.
3. 힙이 빌 때까지 2의 과정을 반복한다.

O(N^2)의 시간 복잡도인 선택 정렬과 유사한 로직이지만 가장 큰 원소를 찾아낼 때 매 번 순회하면서 찾는지 힙을 이용해서 찾는지가 유일한 차이점이다.
힙 정렬은 추가적인 메모리가 전혀 필요없다는 점과 항상 O(NlogN) 정렬의 성능을 발휘하는 장점이 있다. 하지만 실제로는 퀵 정렬이 힙 정렬보다 일반적인 경우에 빠르게 동작한다.

💡 for(int num: pq){sout(num);} 우선순위대로 순회될까?

public static void main(String[] args) {
    PriorityQueue<Integer> pq = new PriorityQueue<>();

    for(int i=0;i<10;i++){
            int temp = (int)(Math.random() * 100); // 0 ~ 100
            pq.offer(temp);
    }

    for(int num : pq){ //넣은 순서
        System.out.println(num);
    }
}

위와 같은 코드를 실행하면 어떤 결과가 나올까? 삽입한 순서? 우선순위에 따른 순회? 실제로 실행해보았다.

-------offer한 순서-------
79
83
50
45
52
2
79
6
10
49
-------실제 enhanced for문으로 순회한 순서-------
2
6
45
10
49
79
79
83
50
52

위 코드를 실제로 실행해보았을 때 삽입한 순서대로 순회하지 않았고, 우선순위 대로 순회하지도 않았다. 그렇다면 순회된 순서는 어떤 기준일까?
생각해보니 힙에서 관리되어지는 배열의 인덱스 규칙처럼 PriorityQueue의 내부는 배열로 구현한 힙을 관리하고 있기 때문에 순서도 배열에 실제 저장되어있는 heapify된 순서대로 출력되는듯 하다.

결론

Java로 알고리즘 문제를 풀 때 유용하게 사용했던 클래스 PriorityQueue에 대해서 살펴보았다. 내부 로직을 얕게 알고 있었지만 로직을 깊게 공부하니 신기하고 재미있는 부분도 있었다. PS에서 자주 쓰이는 다른 클래스들도 천천히 다뤄봐야겠다.

출처

• 힙 트리 - 나무위키
• 정렬 알고리즘 - 나무위키
• Java util 패키지 PriorityQueue.java
• 허프만 코드